Introductory Lab: Domino Size & Density

Introductory Lab: Domino Size & Density#

Background#

Measurements#

Physical measurements are more than a simple numerical value. They are specified by:

A physical dimension which is a product of powers of base physical dimensions such as length, time, and mass. Other dimensions include, for example, electric charge.
A choice of units. Usually we use SI units: meter (m), second (s), and kilogram (kg).
A numerical value that depends on the choice of units.
A range of the numerical value depending on the accuracy of measurements.

Calculations performed using physical quantities follow certain rules:

Scalar physical quantities can be added or subtracted only if they have the same units.
Scalars can be multiplied (or divided). The same action must be performed on the values and on the units.

Volume $V$ and mass $m$ are two measures of the size of an object. If an object is made of a uniform material, then doubling the amount of material will double both its mass and its volume. Density $\rho$ is ratio of mass to volume.

(4)#\[\rho=\frac{m}{V}\]

Density is a material property, independent of the amount of material or shape of the object. The volume of a rectangular parallelepiped shape, i.e., a box, is the product length times width times height, i.e.:

(5)#\[V=l \cdot w \cdot h\]

Estimating Error#

The accuracy of a measurement depends on the limits of the instrument, and on skill in using the instrument. One estimate of the accuracy of a measurement is to independently repeat the measurement multiple times and observe the range and standard deviation of the results. Another approach is to determine the instrument tolerance or precision.

Measurement errors change calculated or derived results in different ways, depending on how the quantities enter equations. For example, if the measured mass is larger than the actual mass, then the calculated density will also be larger. Suppose, on-the-other-hand, that the measured volume is larger than the actual volume. Because the volume appears in the denominator of (4), the calculated density will be reduced.

Experimental Procedure#

OVERVIEW

Understand how to take length and mass measurements.
Understand how to characterize measurement uncertainties due to instrument precision.
Understand how to characterize measurement uncertainties with standard deviation.
Each member of the lab group will independently measure the length, width, height, and mass of four provided dominoes per group (i.e. each lab group gets one pink, one green, one orange, and one blue domino).

Notes

It is good practice to complete the analysis of trials or cases as you do the experiment. If there is some error in your experimental method or in your calculations, you can correct it before completing all the other trials. The rows with their Excel formulas for later trials can be created by copying the first trial.
The density of the dominoes’ plastic and water are roughly the same. Estimate the value you expect in SI units (kg/m³).

../_images/M0_dominos.jpg — Fig. 9 Left) Dominoes provided. Right) Relevant length, width, height dimensions of the dominoes.#

Create data tables (See examples in Common Data and Trial Data):

Create a Common Data Table for values used in all the trials. In this case, include
- the instrumental tolerance or precision of the triple-beam balance
- the instrumental tolerance or precision of the Vernier caliper.
  
  Referencing unchanging values
  
  You can reference these values in these cells with dollar signs to hold the cells constant in your formulas (e.g. $A$1) as needed. Additional info, see Data Analysis with Spreadsheets
Create a Data Table with
- Rows for each domino trial. A trial is the measurement by one lab group member of one domino color. For a group of two, there will be 8 trials; for a group of three, there will be 12 trials.
- Columns for:
  - Trial number
  - Initials of the experimenter
  - Color of the domino
  - Measured length $l$, width $w$, height $h$ (see Fig. 9) measured with Vernier calipers and mass $m$ measured with the triple-beam balance in the instruments’ units (e.g. mm, g, etc.)
  - $l$, $w$, $h$, and $m$ converted to SI units
  - Calculated volume $V_\text{color}$ for the trial in SI units
  - Minimum volume and maximum volume (SI units)
  - Calculated density $\rho_\text{color}$ for the trial in SI units
  - Minimum density and maximum density (SI units)

Run Single Trial with Calculations First (Start to finish of just one trial)

Each group member will independently measure each of the four dominoes (i.e. four trials per person). HOWEVER, start with one domino, then go through all the steps minimizing and maximizing $V$ and $\rho$ before measuring your second domino to ensure your calculations in Excel are behaving properly and that you are actually measuring the dominoes accurately with the calipers and balance. Otherwise, you may find yourselves redoing the whole experiment if you fail to check your measurement techniques early on in the process.

Record the trial number, group member’s name or initials, and the domino color
Using the Vernier calipers (see Reading the Vernier scale), note the caliper’s measurement uncertainty in your common data table (smallest measureable increment, $\delta_{\text{caliper}} = \delta_l = \delta_w = \delta_h$). The Greek letter $\delta$ (said as “delta”) is representing the measurement uncertainty of each variable (e.g. $l \pm \delta_l$). Then measure and record, in the units of the calipers, the:
- length $l$
- width $w$
- height $h$
Using the triple-beam balance, note the balance’s measurement uncertainty (smallest measureable increment, $\delta_m$) in your common data table. Then measure & record the mass $m$, in the units of the balance (e.g. grams).

Convert your measurements into SI units (e.g. kilogram kg, meter m, second s, etc.)

Calculate volume $V$ using (5), and density $\rho$ using (4).

You will now analyze your domino measurements in a few ways, through measurement uncertainties and through average and standard deviation (i.e. the spread of the data from the average).

In your data table, for each trial, calculate the minimized and maximized values for both $V$ and $\rho$.
- To minimize $V$, minimize the values that go into that calculation ($l$, $w$, $h$) by the caliper’s measurement uncertainty in (5) which results in:

(6)#\[V_{\min} = (l-\delta_l)\cdot(w-\delta_w)\cdot(h-\delta_h)\]

Maximize $V$ in a similar manner, now by maximizing $l$, $w$, $h$.
In a similar way, minimize and maximize $\rho$ by using either $V_{\max}$ or $V_{\min}$ with $m$ minimized or maximized.
- e.g. for $\rho_{\min}$, you would minimize the numerator and maximize the denominator such as:

(7)#\[\rho = \frac{m_{\min}}{V_{\max}} = \frac{m-\delta_m}{V_{\max}}\]

At this point, you should have a complete trial with a range of densities based on your measurement uncertainties.

Does this range appear far from your estimated densities from the prior knowledge that these dominoes’ densities are close to that of water? If so, this is a good time to double check any of your measurements that may seem like an outlier or any of your calculations that may have been entered into Excel incorrectly.

Continue to additional trials?

If you are satisfied, it is at this point that each person can now continue measuring the other dominoes.

Up to this point, each individual trial has its own range of densities based on the measurement uncertainties. If we were only analyzing individual trials, this can be satifactory for error analysis. However, each person measured each color domino. We can therefore also analyze the repeated measurements by looking at the average densities and the spread or variation of the data from that average value (i.e. standard deviation, often denoted as the Greek letter sigma, $\sigma$).

We will analyze the data in two ways, first by sorting your data by domino color (across all group members) and by person (across all domino colors). To do so, create two Data Analysis tables including (Analysis Table 1 (by color)):

Analysis Table 1 (by color):
- Average and standard deviations of the length, width, height, mass, volume, and density of each color of domino.
Analysis Table 2 (by person):
- Average and standard deviations of the length, width, height, mass, volume, and density of the color set measured by each lab group member.

Based on your data, do you expect some or all of the dominos to float, sink, or stay neutrally buoyant in room-temperature water? Before you leave, there should be a bucket of water near the front of the lab, test it out!

Post-Lab Submission — Interpretation of Results#

Make sure to submit your finalized data table (Excel sheet).
In a paragraph, summarize the results you have determined in each case. Consider:
- What were your densities for each of the different colored dominoes (based on Analysis Table 1), and did each color agree (within experimental uncertainty assuming the use of standard deviation $\sigma$ as our uncertainty)? In other words, do all the $\rho_{\text{blue-person1}}\pm\sigma_{\text{blue-person1}}$, $\rho_{\text{blue-person1}}\pm\sigma_{\text{blue-person2}}$, etc. agree?
- Are the average densities of all four dominoes as measured by each person consistent (within experimental uncertainty assuming the use of standard deviation $\sigma$ as our uncertainty)? (i.e. do all the $\rho_{\text{blue-person1}}$, $\rho_{\text{green-person1}}$, etc. agree?)
- Based on your measurements, did you expect the dominoes to float in water (at room temperature)? Did you test it? What did you find, confirmation or disconfirmation of your predictions?
In a paragraph, summarize your error analysis. Be qualitative not only quantitative.
- What was the precision of your equipment (calipers, triple-beam balance, etc.)?
- What are possible systematic errors for today’s experiments?
- How might your values of $\rho$ change based on those uncertainties?
- How does the range of densities for an individual domino trial based on measurement uncertainties (i.e. $\rho_{\text{min}}$ and $\rho_{\text{max}}$) compare to the range of densities given by the standard deviation $\sigma$ across colors or across group members?
  - Larger or smaller? IWhat does this comparison imply about the main sources of error in this experiment?

The Whiteboard#

Example data tables are shown below to assist you in building your spreadsheet for this first lab. Additionally the original whiteboard summary is at the end of this section.

Common Data#

Variable (units)	Value
Mass uncertainty (SI units)
Caliper uncertainty (SI units)

Trial Data#

Trial number	Group Member Initials	Color
1	AB	pink
2	AB	green
3	AB	orange
4	AB	blue
5	CD	pink
6	CD	green
7	CD	orange
8	CD	blue
9	EF	pink
10	EF	green
11	EF	orange
12	EF	blue

Analysis Table 1 (by color)#

	Length (units)	Width (units)	Height (units)	Mass (units)	Volume (units)	Density (units)	Did it float?
Avg pink
Avg green
Avg orange
Avg blue
Stdev pink
Stdev green
Stdev orange
Stdev blue

Analysis Table 2 (by person)#

	Length (units)	Width (units)	Height (units)	Mass (units)	Volume (units)	Density (units)
AB avg
AB stdev
CD avg
CD stdev
EF avg
EF stdev

Original Whiteboard Info#

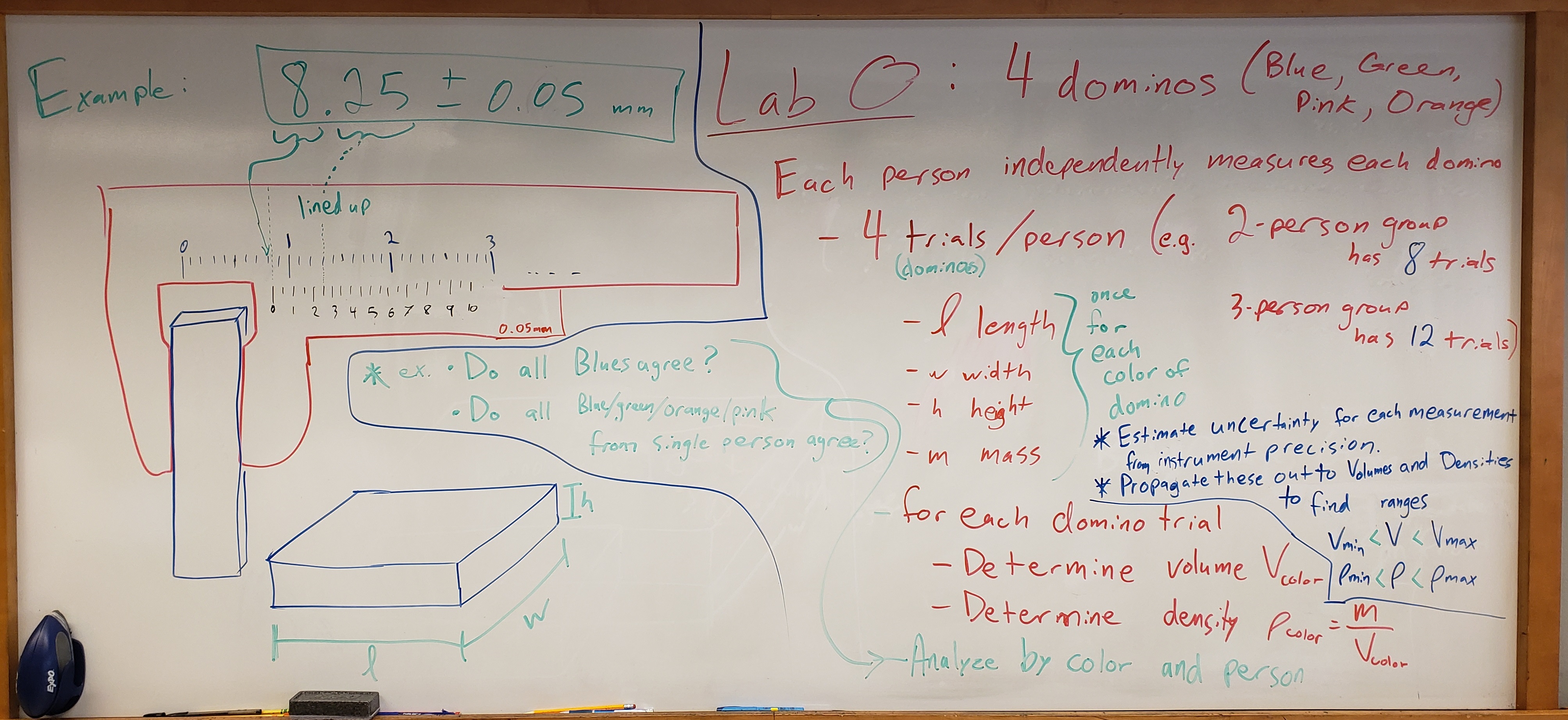
../_images/IntroDominos_2024_Fall_01.jpg — Fig. 10 Original whiteboard summary#